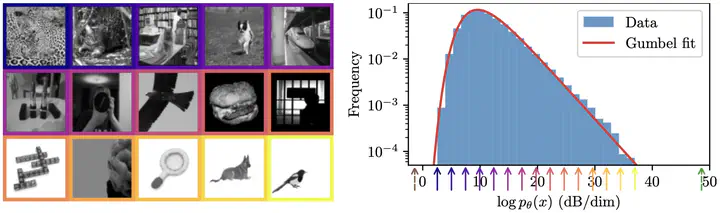
Abstract
Learning probability models from data is at the heart of many learning tasks. We introduce a new framework for learning normalized energy (log probability) models inspired from diffusion generative models. The energy model is fitted to data by two “score matching” objectives: the first constrains the gradient of the energy (the “score”, as in diffusion models), while the second constrains its time derivative along the diffusion. We validate the approach on both synthetic and natural image data: in particular, we show that the estimated log probabilities do not depend on the specific images used during training. Finally, we demonstrate that both image probability and local dimensionality vary significantly with image content, challenging simple interpretations of the manifold hypothesis.
Florentin Guth
Postdoctoral Researcher in Science of Deep Learning
I’m a Faculty Fellow in the Center for Data Science at NYU and a Research Fellow in the Center for Computational Neuroscience at the Flatiron Institute. I’m interested in improving our scientific understanding of deep learning, e.g., explaining how it escapes the curse of dimensionality, particularly in the context of image generative models.